3A) Bezier curves

Exercises Explain what C0-, C1-, C2-, Cn-continuity mean. Derive the constraints on control point positions which ensure that two quartic Bezier curves join with (a) C0-continuity, (b) C1-continuity, and (c) C2-continuity.

3B) B-splines.

Why B-splines?

• minimise the order of the polynomial pieces (order k)
• maximise the continuity between pieces (continuity C(k-2))
• minimise the number of control points controlling a piece (k points)
• have positive basis functions
• have basis functions which partition unity, implying that each piece lies inside its control points' convex hull
• are invarient with respect to affine transforms

Exercises How many control points are required for a quartic Bezier and how many for a quartic B-spline? Why are cubics the default for B-spline use? Explain the difference between Uniform, Open Uniform, and Non-Uniform knot vectors. What are the advantages of each type?

3C) NURBS

Non-uniform rational B-splines are the curves that are currently used in any graphics application that requires curves and surfaces with more functionality than Bezier curves can offer. In addition to the features listed in Part 3B, NURBS are invarient with respect to perspective transforms.

NURBS curves incorporate -- as special cases -- uniform B-splines, non-rational B-splines, Bezier curves, lines, and conics. NURBS surfaces incorporate planes, quadrics, and tori.

Exercises Review from IB: What are homogeneous coordinates and what are they used for in computer graphics? Explain how to use homegeneous coordinates to get rational B-splines given that you know how to produce non-rational B-splines. Convince your supervisor that you understand why NURBS includes Uniform B-splines, Non-Rational B-splines, Beziers, lines, conics, quadrics, and tori. When would you use Bezier curves and when would you use B-splines? (i.e. why have B-splines, in general, replaced Bezier curves in CAD?) [1998/7/12] Consider the design of a user interface for a NURBS drawing system. Users should have access to the full expressive power of the NURBS representation. What things should users be able to modify to give them such access and what effect does each have on the resulting shape? For each of the items (in the previous question) that the user can edit: (i) Give sensible default values; (ii) Explain how they would be constrained if a `demo' version of the software was to be limited to cubic Uniform Non-rational B-Splines. [1999/7/11] (c) Show how to construct a circle using non-uniform rational B-splines (NURBS). (d) Show how the circle definition from the previous part can be used to define a NURBS torus. [You need explain only the general principle and the location of the torus' control points.]

4A) Generative models

Sweeps

Surfaces of revolution are covered in R&A section 6-2. Sweeps are covered in R&A section 6-3 and FvDFH section 12.4. Parts of Sections 6-2 and 6-3 of R&A are included in the handout.

Extrusion

Surface of revolution

Revolution or extrusion?

General sweeps

• Cross section
  Some two dimensional shape that is to be swept along the sweep path. It does not have to be circular. At right are two swept objects, one with a circular cross-section, one with a polygonal cross-section.
  
• Sweep path
  The path along which the two dimensional cross section is swept to produce the three dimensional shape. It may be any curve. At right we see two views of the same swept object: a polygonal cross-section is swept along a convoluted path.
  
• Twist
  How the cross section twists (rotates) as it moves along the sweep path. The default would be to have no twist at all. At right is a swept object with and without some twist.
  
• Scale
  
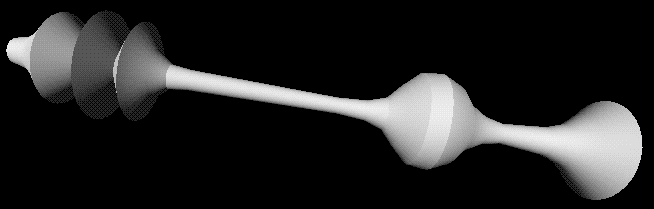
  How the cross section scales (changes size) as it moves along the sweep path. The default would be to have it stay the same size along the whole path. Above are a cylinder, and the same cylinder with different scales along its length.
  
• Normal vector direction
  The normal vector of the 2D cross section will usually point along the sweep path at each point. Changing this will change the nature of the swept object. See R&A Figure 6-17 (in the handout) for an example.

You may be able to think of parameters, other than those in the list above, which could be modify.

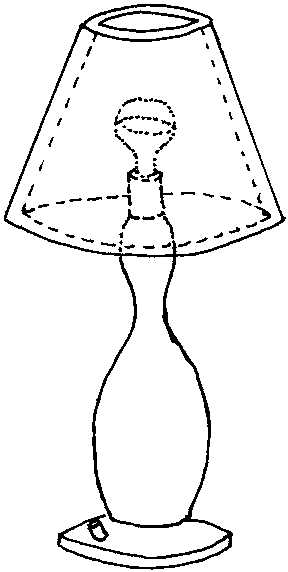
Exercises [1998/7/12] Show how the following object can be represented as a swept object. Use the following different methods of specifying a geometrical model for this picture (assuming it's a three dimensional model and not a line drawing). Come as close as you can to the original for any of the methods, and describe the difficulties in using a particular method for this model. Extrusions Surfaces of revolution General sweeps For each of the following categories list five real-world objects which could be represented by the primitives in the category. The ray-tracing primitives in Part 2A Extrusions Surfaces of revolution General sweeps A flume (water tunnel) at a swimming complex is modeled as a circle swept along a particular path. The designers also want to model the volume swept out by a person traveling down the flume. (We can approximate the cross-section of a person with something roughly elliptical and we'll assume the `virtual' person doesn't move legs or arms while hurtling along.) Explain which parameters in the list would be need to be modified to specify the shape of the flume and which would need to be modified to model the volume swept out by a person traveling down the flume (alternatively, specify which parameters would be held constant, in each case, for the entire length of the sweep).

4B) Converting swept objects to polygons

Swept objects are hard to ray trace. Imagine trying to write a ray/object intersection algorithm for a general swept object. This means that we generally need to polygonise swept objects in order to render them. For PSC we obviously must convert them to polygons.

A swept surface may be easily converted to polygons by converting the outline of the 2D cross section to a polygon, and converting the sweep path to connected set of line segments. Moving the polygon to each vertex of the set of line segments, and connecting vertices accordingly, will produced a polygon mesh which approximates the swept surface.

Exercises [1998/7/12] Show how to convert the swept object from Part 4A Exercise 1 into polygons. What extra work would you need to do if you had to convert it into triangles?

4C) Constructive Solid Geometry

CSG is covered in FvDFH sections 12.7 and 15.10.3.

The following example illustrates the three CSG operations in use on simple three dimensional primitives.

The two primitives: a sphere and a box.
The union of the two primitives.
The intersection of the two primitives.
The difference of the two primitives: box minus sphere.

The following example, based on FvDFH Plate III.2, shows an object for which CSG is (probably) the only sensible modelling technique. The object rendered in the right-hand image is constructed from the primitives shown in the left-hand image. It is mostly made out of cylinders, but you will recognise the extruded star from Part 4A.

At right, I tried the "Godel, Escher, Bach" treatment on my initials. Unfortunately the letters N, A, and D are not as amenable to this as the letters G, E, and B: notice that the shadow of the N has a slight curve at its top right, owing to the N's intersection with the curve on the D and the slope on the A. Various other arrangements of the three letters were tried, all of which gave more noticable artefacts than this. Each of the letters is a CSG object (the D, for example, is constructed from cylinders and boxes). The final effect is produced simply by intersecting the three letters.

Exercises Work out how to represent a Lego technic brick as a CSG object. You may assume that you have box and cylinder primitives. [1998/7/12] Work out how to represent the following object using CSG. You may assume the following primitives: sphere, cylinder, cone, torus, box. [1999/9/4] (c) List the three ways of combining objects using constructive solid geometry (CSG). Describe how an object built using CSG can be represented using a binary tree. Given the intersection points of a ray with each primitive in the tree, explain how these points are passed up the tree by each type of combination node to produce a list of intersection points for the whole CSG object.

4D) Implicit surfaces, voxels and the marching cubes algorithm

Implicit surfaces

Voxels and the marching cubes algorithm

Exercises Give a definition of an implicit surface and give three examples of where such things might be useful. The marching cubes algorithm, as it applies to implicit surfaces, is described in the Wyvill article; while Lorenson and Cline concentrate on the algorithm as applied to voxel data. It is useful that the same algorithm works for both types of data. Explain how voxel data can be thought of a defining an implicit surface (or surfaces). Explain, conversely, how the Wyvill algorithm can be thought of as converting implicit surface data into voxel data before producing the final surface. Following Section 4 of Lorenson and Cline's paper, sketch an implementation of the two-dimensional `marching squares' algorithm -- where you generate line segments in 2D rather than triangles in 3D. An appliation of this algorithm would be the drawing of isobars on a weather map, given pressure values at a regular (2D) grid of points. Medical data is captured in slices. Each slice is a 2D image of density data. The distance between slices may be different to the distance between the pixels within a slice (for example, see Lorenson and Cline, Section 7.1, p. 167). What effect does this difference have on the voxel data? What effect does it have on the marching cubes algorithm? Consider Lorenson and Cline, Section 6. This research was done about twelve years ago. Given your knowledge of processor performance, what differences in performance would you expect to see between then and now? Lorenson and Cline is an example of a graphics research paper. Critically evaluate Lorenson and Cline. How good is this piece of research? Research papers at the SIGGRAPH conference are limited in their length. Evaluate Lorenson and Cline in terms of the following questions. What has been left out that would have been useful? What has been included that could have been left out? Where could the explanation have been better? Are any of the figures extraneous? Where would an extra figure have been helpful? List any grammatical or spelling errors (there is at least one of each).

5) Radiosity

Exercises Explain what lighting effects radiosity is trying to model that are not modelled by RT or PSC. Describe the basic radiosity algorithm. [1999/9/4] (d) Explain what a form factor is, in radiosity. Outline an implementable method of calculating form factors.

Human-Computer Interaction

Exercises These exercises relate to Parts 6 and 7 of the syllabus. Fitts' Law: What changes when you have older users? When you measure the speed with which someone can move their elbow? When you measure underwater? Rate the importance of: Speed of Use, Computational Resources, Ease of Learning, Ease of Rememberance, Error Potential for the following applications: Airplane autopilot controls Word processor Push bar on exit door VCR Mechanical pencil Air traffic control display Quake keyboard control Write out the steps in the Goals loop (i.e. intention, specificiation... etc.) for the following goals: Adding 2 + 4 on a calculator Signalling a turn in a car Which part of the Goals loop are difficult to measure and why? In an example in the HCI lectures the speed of emboldening a word using keystrokes and the menu is compared. Develop a similar speed evaluation for using a toolbar button to embolden a word. State which method you think is best and why. Do you see any problems inherent in treating the human as a processor? Would you call user interface design an art? Why or why not? [1999/9/4] (a) Describe the Model Human Processor. (b) Explain the limitations of the Model Human Processor. Other Past Exam Question: Be brief, and answer only the stuff that is covered in this lecture course (i.e. conceptual model, keystroke model, Fitts' and Hick's Laws, interaction styles): 1993/9/5, 1994/9/6, 1995/7/13, 1996/8/10.